Enhancing Mathematical Reasoning in LLMs with Background Operators
Jiajun Chen, Yik-Cheung Tam·December 05, 2024
Summary
The paper introduces using background operators for enhancing mathematical reasoning in large language models. It defines fundamental mathematical predicates as building blocks and develops Prolog solutions for problems, incorporating problem-specific and derived predicates. The MATH-Prolog corpus, derived from MATH corpus counting and probability categories, is used for efficient data augmentation through K-fold cross-validated self-training. This method generates new Prolog solutions, improving accuracy to 84.6% on cross-validation and 84.8% on testing during Meta-Llama-3.1-8B-Instruct model fine-tuning. The approach uncovers new, fully computable solutions for unseen problems and enhances solution coverage by integrating background mathematical predicates into prompts.
Introduction
Background
Overview of large language models and their capabilities
Importance of mathematical reasoning in AI applications
Objective
Aim of the paper: integrating background operators for improved mathematical reasoning
Expected outcomes: enhanced accuracy and solution coverage
Method
Data Collection
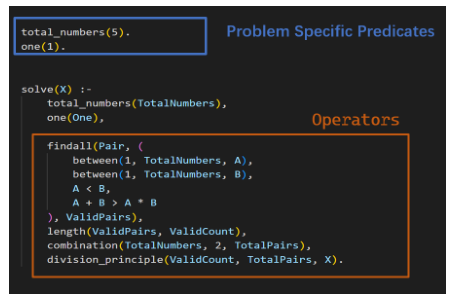
Source of data: MATH-Prolog corpus derived from MATH corpus counting and probability categories
Methodology: efficient data augmentation through K-fold cross-validated self-training
Data Preprocessing
Description of preprocessing steps for the MATH-Prolog corpus
Techniques used for preparing data for model fine-tuning
Model Fine-tuning
Selection of the Meta-Llama-3.1-8B-Instruct model for fine-tuning
Process of integrating the MATH-Prolog corpus into the model training
Evaluation metrics: accuracy on cross-validation and testing
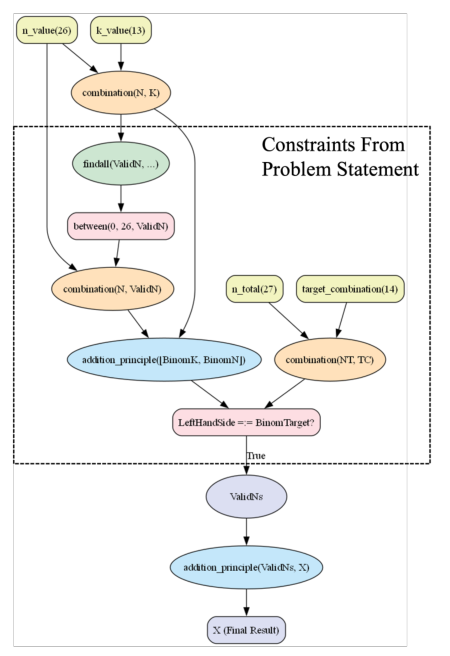
Integration of Background Mathematical Predicates
Explanation of how background operators are incorporated into prompts
Benefits: discovery of new, fully computable solutions for unseen problems
Impact on solution coverage
Results
Accuracy Improvement
Detailed results on accuracy improvement during model fine-tuning
Comparison of accuracy before and after integrating background operators
Solution Coverage Enhancement
Analysis of increased solution coverage achieved through the integration of background mathematical predicates
Examples of improved problem-solving capabilities
Conclusion
Summary of Findings
Recap of the paper's main contributions
Implications
Discussion on the broader implications for AI and mathematical reasoning
Future Work
Suggestions for further research and potential improvements
Basic info
papers
artificial intelligence
Advanced features