A Unified Differentiable Boolean Operator with Fuzzy Logic

The paper introduces a unified differentiable boolean operator for implicit solid shape modeling using Constructive Solid Geometry (CSG). This operator, inspired by fuzzy logic, outputs a continuous function and is differentiable with respect to operator types, enabling optimization of both primitives and boolean operations using continuous optimization techniques like gradient descent. The proposed operator allows modeling of both sharp mechanical objects and smooth organic shapes with the same framework, opening possibilities for future research in fully continuous CSG optimization. 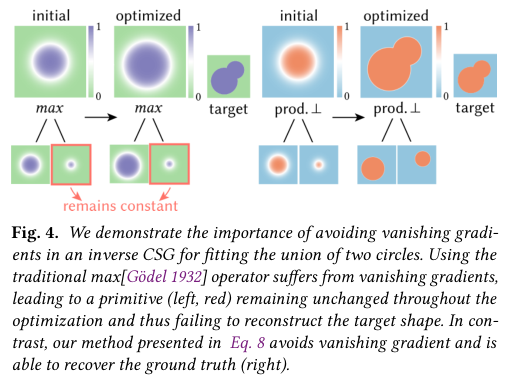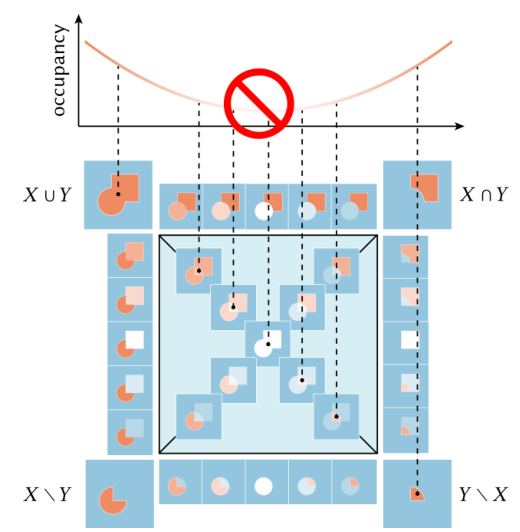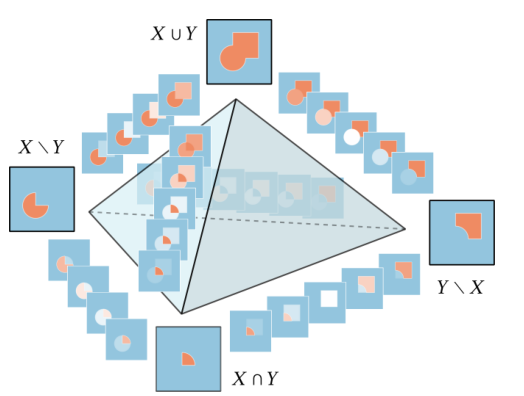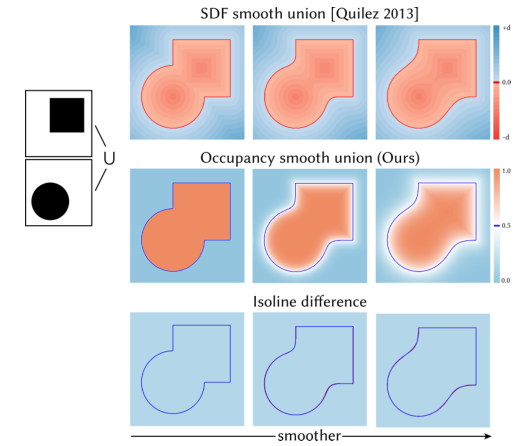The paper also discusses a differentiable boolean operator for inverse CSG optimization, which allows continuous switching between boolean operations like union and difference, unlike traditional methods that fix the structure of the CSG tree. The unified operator uses tetrahedral barycentric interpolation to combine individual fuzzy boolean operations, ensuring the result remains a soft occupancy function. This operator is differentiable, avoids vanishing gradients, and is monotonic, making it suitable for gradient-based optimization. 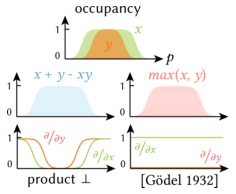The text further explores the use of fuzzy logic operations in computer graphics and solid modeling, introducing fuzzy union, fuzzy complement, and fuzzy difference, defining their properties and common functions. The focus then shifts to product fuzzy logic, which meets criteria for differentiability and non-vanishing gradients, making it suitable for continuous optimization. The text also addresses the issue of vanishing gradients, which can hinder optimization, and highlights the benefits of product fuzzy logic in avoiding this problem. 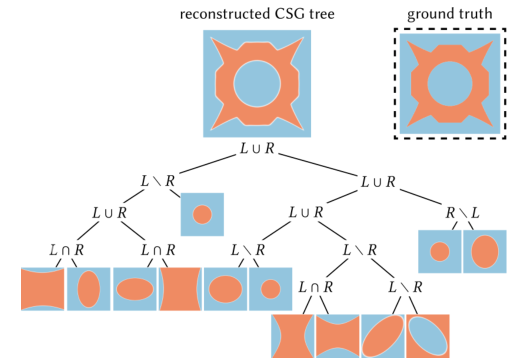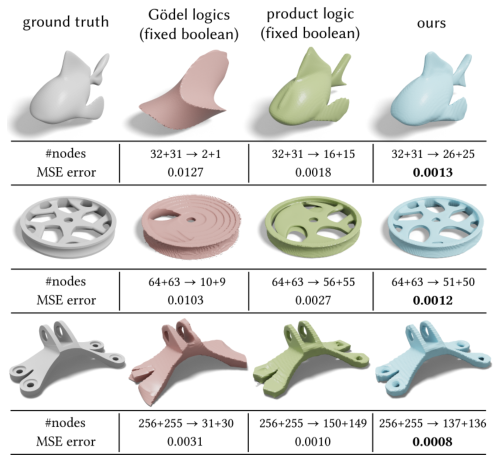The paper introduces a unified differentiable Boolean operator with fuzzy logic for fitting and optimizing complex shapes. This operator allows for the conversion of shapes into CSG trees using various primitive families, such as spheres, planes, quadrics, and neural networks. The method optimizes both primitive parameters and boolean nodes, leading to better reconstruction compared to fixing boolean nodes and only optimizing primitive parameters. The approach is independent of the choice of primitive families and results in more compact full binary CSG trees after pruning redundant nodes. The paper also discusses various research papers and articles related to the field of computer graphics, focusing on the development and application of Boolean operators, fuzzy logic, and constructive solid geometry (CSG). The research covers a range of topics, including learnable convex decomposition, unsupervised learning of shape programs, automatic conversion of 3D models to CSG trees, and optimization of CSG tree extraction. The papers highlight advancements in algorithms, methodologies, and applications in computer graphics, aiming to improve the efficiency, accuracy, and interpretability of 3D modeling and rendering techniques. In conclusion, the paper presents a unified differentiable boolean operator for solid shapes with soft occupancy, enabling optimization of both primitives and boolean operations. This operator improves the fitting and optimization of complex shapes, leading to better reconstruction and more compact full binary CSG trees. The research also explores the application of fuzzy logic to CSG modeling, evaluating fuzzy counterparts of existing CSG operations and suggesting the addition of new operators. Future work includes exploring applications of fuzzy logic beyond CSG and developing better neural network architectures for tree generation.